Wpisy do indeksu; 4 lutego; godzina 11:00-14:00; B3-13!!!

WWW site; ten sam termin!!!

Projekty Grupowe:

• Badanie K-spojnosci grafow, Jakub Sochacki, Pawel Konieczka, Przemyslaw Sokolowski
• Okreslanie podobienstwa stringów przy uzyciu programowania równoleglego, Pawel Kobzdej, Dariusz Waligóra, Kinga Wielebinska
• Mnozenie macierzy - algorytmy równolegle, Filip Stachecki, Lukasz Sosnowski, Bartosz Nowicki
• Powloka wypukla, Korpik Maciej, Okolowski Dariusz, Robaszkiewicz Tomasz
• Symulator ruchu ukladów gwiezdnych, Maciej Gawinecki, Pawel Kaczmarek, Andrzej Dopierala
• Wykorzystanie algorytmów znajdowania skojarzen w grafach do procesu przydzialu zadan i planowania zatrudnienia, Maciej Chrósniak, Jakub Dworniczak, Karol Ziarko
• Ray Tracing, Tomasz Ciesielski, Michal Giertych, Dominik Zalewski
• Znajdowanie najwiekszego skojarzenia w grafie wazonym, Rafal Jeziorny, Maciej Jaroszewski, Maciej Kalkowski
• Inteligentna kompresja bazy danych, Jakub Berlinski, Cezary Rzepecki, Maciej Jaskiewicz
• Efektywna Równolegla Implementacja Wybranych Algorytmów Ewolucyjnych, Onak Tomasz, Prochowicz Krzysztof, Tomiak Dominik
• Identyfikacja daktyloskopijna, Pawel Bakowski, Krzysztof Chmiel, Dariusz Czech
• Rownolegly Automat Komorkowy, Radomir Dopieralski, Justyna Walkowska, Daniel Szewczyk, Sebastian Lenarczyk
• Przepływy w sieciach, Bartlomiej Misiak, Piotr Stefanski, Michal Wlodarczyk, Piotr Zbyszynski

Użyteczne linki:

• Kurs z USM
• Polskojęzyczne wprowadzenie do MPI

Omawialiśmy:

1. Geneza programowania równoległego:

• konieczność rozwiązywania dużych problemów
  • modelowanie pogody
  • rozwiązywanie zagadnień o dużych macierzach gęstych
  • modelowanie wybuchów jądrowych
• nie istnieje maszyna jednoprocesorowa zdolna do efektywnego rozwiązania zagadnień tego typu o praktycznej stosowalności; główne ograniczenia:
  • prędkość procesora
  • wielkość dostępnej pamięci
  • wielkość dostępnych nośników pamięci zewnętrznej i prędkość dostępu do nich

2. Początki maszyn wielkiej mocy

• cykl pobierz-wykonaj
• linia produkcyjna (ang. pipelining )
• niezależne linie produkcyjne dla danych
  • rałkowitoliczbowych
  • zmiennoprzecinkowych
• niezależne linie produkcyjne dla
  • dodawania
  • mnożenia
• procesory wektorowe
• łączenie w łańcuch operacji dodawania z operacją mnożenia ( y = ax+b )
• zwiększenie liczby linii produkcyjnych w jednym procesorze np.:
  • 4 linie całkowitoliczbowe
  • oraz
  • 2 linie zmiennoprzecinkowe
• wynik procesu: każdy nowoczesny procesor jest komputerem równoległym
• nowoczesne procesory za szybkie dla pamięci - wynikiem: pamięć hierarchiczna
• wpływ pamięci hierarchicznej na pisanie programów – przykład mnożenia macierzy

3. Równoległość

• Dowolne ulepszenia zaproponowane w 2. są niewystarczające. Koniecznym jest łączenie wielu procesorów w jedno środowisko obliczeniowe.
• Podział komputerów wg. Flynn’a, czyli podział ze względu na ilość strumieni danych i ilość strumieni instrukcji
  • Jeden strumień instrukcji i jeden strumień danych (ang. Single Instruction Single Data; SISD) – standartowy model komputera zaproponowany przez von Neumann’a.
  • Wiele strumieni instrukcji i jeden strumień danych (ang. Multiple Instruction Single Data; MISD) – w zasadzie trudno wskazać na odpowiadający temu modelowi komputer (różni autorzy czynią różne sugestie, ale nie ma zgody)
  • Jeden strumień instrukcji i wiele strumieni danych (ang. Single Instruction Multiple Data; SIMD) – popularny model komputerów występujących w latach późnych latach 80tych i wczesnych latach 90tych
    • macierz procesorów (raczej słabych; nawet 1-bitowych)
    • osobna maszyna-kontroler (kompilacja i zarządzanie wykonaniem programu)
    • poszczególne procesory wykonują tę samą operację na różnych danych (lub w danym kroku nie wykonują żadnej operacji)
    • łatwo tworzyć programy gdy domena daje się w prosty sposób reprezentować jako prostokąt
    • problemy z elastycznością (np. domeny „dowolne”) – spowodowały zanik komputerów SIMD w połowie lat 90tych
    • obecnie macierze procesorów stosowane są do przetwarzania obrazów (komputery specjalne) lub też stają się częścią najnowocześniejszych procesorów (instrukcje MMX w procesorach Intel)
  • Wiele strumieni instrukcji i wiele strumieni danych (ang. Multiple Instruction Multiple Data; MIMD) – powszechnie stosowany obecnie typ komputerów równoległych
    • Występuje w dwu podgatunkach – z pamięcią wspólna (ang. shared memory) i z pamięcią rozproszoną (ang. distributed memory)
    • Komputery z pamięcią wspólną
      • Najprostszy model – wczesne komputery – procesory połączone z pamięcią globalną (fizyczną i logiczną)
      • Model „pełny” – procesory z pamięcią typu cache (jedno lub dwupoziomową) połączone z pamięcią globalną (fizyczną i logiczną) – prowadzi do problemów związanych z ustaleniem gdzie znajdują się aktualne kopie danych (ang. cache coherency problem) – istotny aktualnie rozważany problem badawczy
      • Połączenie pomiędzy procesorami
        • magistrala (ang. bus)
        • przełączniki (ang. switch): omega, butterfly, crossbar, optyczny
      • Główny problem – bez względu na stosowane połączenie pomiędzy procesorami a pamięcią istnieje górna granic ilości procesorów, które można tak połączyć i w zasadzie pozostaje ona nie zmieniona; za wyjątkiem specjalnych przełączników stosowanych przez firmę IBM i dających możliwość połączenia do 64 procesorów, górną granicą są 32 procesory
    • Komputery z pamięcią dzieloną
      • Każdy „procesor” takiego komputera to procesor połączony z lokalną pamięcią – nie istnieje pamięć globalna (fizyczna ani logiczna)
      • Poszczególne procesory połączone są przy pomocy „sieci”
      • Najpopularniejsze topologie:
        
        • hipersześcian
        • pierścień
        • siatka
        • obwarzanek (ang. torus)
        • topologie hierarchiczne (drzewka o skomplikowanej strukturze)
      • Główny problem – programista musi „osobiście” zajmować się zarządzaniem lokalizacją i przesyłem danych.
    • Komputery o architekturze mieszanej – tworzenie komputerów o pamięci dzielonej składających się z hierarchicznie zorganizowanych komputerów o pamięci wspólnej – np. każdy z komputerów połączonych w pierścień jest komputerem o pamięci wspólnej i 16 procesorach; następnie wiele pierścieni połączonych zostaje w pierścień wyższego rzędu; jest to architektura komputera firmy KSR; podobne komputery – o innej topologii hierarchicznej powstają również obecnie (np. wyroby formy IBM).

4. Programowanie komputerów równoległych

• Komputery a pamięcią wspólną
  • Podstawowa metoda zrównoleglania programów – dzielenie pętli; w przypadku pętli zagnieżdżonych, najlepiej dzielić pętlę najbardziej zewnętrzną (wyjaśnienie podane zostanie gdy rozważać będziemy efektywność programów równoległych).
  • Początkowo każdy wytwórca komputerów równoległych z pamięcią wspólną stosował własny zestaw operacji i ich nazw (choć ich funkcjonalność była bardzo podobna), jednakże większość z nich miała postać komend, które mogą być ignorowane przez standartowe kompilatory sekwencyjne (np. komendy zaczynające się od symbolu wyznaczającego komentarz).
  • W chwili obecnej podejścia to zostały ujednolicone w standardzie OpenMP
  • Możliwym jest również stosowanie podejść takich jak dla komputerów z pamięcią dzieloną (poniżej)
• Komputery z pamięcią dzieloną
  • Pierwsze próby – każdy wytwórca proponował swoje własne komendy przemieszczania danych i synchronizacji operacji
  • Pierwszy standard – PVM; skierowany na interaktywne tworzenie komputera równoległego; umożliwiający tworzenie komputerów heterogenicznych (składających się z różnorodnych procesorów/węzłów); w chwili obecnej w zasadzie zamiera
  • Aktualny standard – MPI; większa ilość funkcji systemu przeniesiona do poziomu otoczenia programowego MPI (np. definiowanie procesorów wchodzących w skład komputera); w zasadzie większość programów wykonywanych aktualnie na superkomputerach pisana jest używając MPI jako biblioteki komunikacji pomiędzy procesami i synchronizacji operacji
• Komputery hybrydowe – o pamięci wspólnej i dzielonej
  • Możliwość 1 – zastosowanie MPI – rozwiązanie skuteczne i nie wymagające dodatkowej pracy; często stosowane
  • Możliwość 2 – stosowanie OpenMP i traktowanie pamięci jako wirtualnej pamięci wspólnej; problem – możliwa utrata efektywności
  • Możliwość 3 – stosowanie OpenMP na węzłach będących komputerami z pamięcią wspólną i MPI „pomiędzy” nimi; OpenMP współpracuje z MPI; więcej pracy dla programisty; możliwe pełne wykorzystanie mocy obliczeniowej komputera (maksymalizacja efektywności implementacji)

Prace domowe:

PRACA DOMOWA 1 (grupowa)
Po pierwsze, proszę o utworzenie grup 3-osobowych. Po drugie, każda grupa musi uzgodnić ze mną temat projektu semestralnego. Temat ten powinien zostać zatwierdzony do piątku, 10 października, 2003; o godzinie 23:55. Po czwarte (rzeczywista praca domowa), każda grupa tworzy WWW-site projektu semestralnego i dostarcza mi "link" (e-mailem) do tejże strony; do 17 października, godzina 23:55 (będę sprawdzał "time-stamp" otrzymania wiadomości na mojej maszynie). WWW-sites będą oceniane pod względem treści i formy. Każda osoba w grupie otrzyma tę samą ocenę.

PRACA DOMOWA 2 (grupowa)
W dniu 22 października na ćwiczeniach każda grupa zaprezentuje wstępne założenia projektu semestralnego. Każda prezentacja powinna mieć 8 minut + 2 minuty na dyskusję. Prezentacje powinny być "profesjonalne" (nabazgranie czegoś na tablicy nie jest prezentacją profesjonalną). Prezentacje będą oceniane pod względem treści i formy. Każda osoba w grupie otrzyma tę samą ocenę.

PRACA DOMOWA 3 (indywidualna)

Otrzymaliście Państwo konta na maszynie tulipan. Na poprzednim wykładzie omawialiśmy 6 wersji mnożenia macierzy i ich potencjalny wpływ na efektywność obliczeń. Celem pracy domowej będzie empiryczne sprawdzenie hipotez postawionych w czasie wykładu. W tym celu należy zaimplementować program wykonujący (bezbłędnie) wszystkie 6 wersji mnożenia macierzy. Równocześnie koniecznym będzie użycie zegara systemowego umożliwiającego ustalenie rzeczywistego zużycia czasu (CPU time vs. Wall-clock time).

Następnie należy ustalić jaki rozmiar macierzy jest już dostatecznie duży aby można było założyć, że wskazania zegara mają sens (wskazania zegara w pobliżu jego rozdzielczości są podejrzane!); proszę zaokrąglić rozmiar macierzy do „ładnego” rozmiaru – rozmiar minimalny.

Następnie należy ustalić maksymalny rozmiar macierzy; taki, dla którego czas mnożenia wynosi około dwu minut i również zaokrąglić tenże rozmiar do „ładnej” liczby – rozmiar maksymalny.

Przedział pomiędzy macierzą minimalna i maksymalną należy podzielić na podprzedziały o równej długości tak, aby otrzymać 8 punktów pomiarowych (przypadających dla „ładnych” rozmiarów macierzy) i dokonać pomiaru czasu mnożenia. Należy zastosować maksymalną optymalizację dostępną w kompilatorze, oraz każdy pomiar powinien być dokonany przynajmniej 3 razy aby wyeliminować fluktuacje spowodowane różnorodnymi czynnikami związanymi z otoczeniem w którym program jest wykonywany.

Wynikiem ma być raport – coś w rodzaju artykułu – w standartowym formacie: tytuł, wprowadzenie, metodologia, wyniki i ich analiza, konkluzje, literatura.

Termin wykonania pracy domowej i metoda dostarczenia: godzina 15:00 (czasu Polskiego), w piątek 14 listopada, 2003; tekst w formacie: pdf, doc, rtf lub ps, przesłany e-mailem do mnie: marcin.paprzycki@ibspan.waw.pl.

PRACA DOMOWA 4 (indywidualna)

1. Oprogramować adaptacyjną równoległą metodę całkowania numerycznego omówioną w czasie ćwiczeń.
2. Testowanie efektywności metody przeprowadzić dla funkcji f(x) = sin(kx) * e^(x/4) + π – 2.0, na przedziale [0, 15π] gdzie k jest jednym z parametrów zagadnienia; drugim jest liczba procesorów p (warunek końcowy dla iteracji: EPS = 0.001).
3. Przetestować efektywność zrównoleglenia procedury całkowania dla zmieniających się wartości k i dla p = 1,2,..., 12
4. Proponowana miara efektywności to przyspieszenie (speedup); czyli stosunek czasu wykonania programu na jednym procesorze do czasu wykonania programu na p procesorach.
5. Wynikiem ma być raport – w standartowym formacie: tytuł, wprowadzenie, metodologia, wyniki i ich analiza, konkluzje, literatura (zawierający kod jako zalącznik/appendix)
6. Termin wykonania pracy domowej i metoda dostarczenia: na ćwiczeniach we środę 10 grudnia, 2003; wydruk dostarczony osobiście do mnie.

PRACA DOMOWA 5 (indywidualna)

Na zajęciach (ćwiczenia) omawialiśmy problem „wyboru przewodniczącego” w asynchronicznym pierścieniu, w którym każdy z uczestników zna tylko swoich sąsiadów po lewej i prawej stronie (nie posiada żadnej innej wiedzy o systemie). W rozdanych materiałach znajdują się dwa algorytmy rozwiązywania tego problemu różniące się ilością przesyłanych wiadomości (zakłada się tutaj, że złożoność algorytmu wyboru przewodniczącego jest zależna od ilości przesyłanych wiadomości). Jeden z nich ma złożoność n² a drugi złożoność nlogn. Celem pracy domowej jest porównanie obu algorytmów zaimplementowanych używając biblioteki komunikacyjnej MPI i wykonywanych na „tulipanie”.  Tak wiec należy

• Zaimplementować oba programy
• Przetestować je dla wirtualnych pierścieni o rozmiarach dostatecznie dużych aby zegar był w stanie zmierzyć czas (pierścienie muszą być wirtualne, albowiem trzeba będzie użyć o wiele więcej uczestników niż dostępnych w systemie procesorów)
• Napisać raport opisujący wyniki eksperymentów – jak w poprzednich pracach domowych
• W ramach raportu powinienem dostać również (jak załącznik) kod zaimplementowanego algorytmu

UWAGA: w eksperymentach i raporcie proszę wziąć pod uwagę moje uwagi na temat Państwa prac wygłoszone na jednym z ostatnich wykładów – mam nadzieję, że tym razem będą to o wiele lepsze raporty, albowiem poprzeczka oceny idzie w górę!!!!

Termin wykonania pracy domowej i metoda dostarczenia: godzina 20:00 (czasu Polskiego), w piątek 9 stycznia, 2004; tekst w formacie: pdf, doc, rtf lub ps, przesłany e-mailem do mnie: marcin@amu.edu.pl.

PRACA DOMOWA 6 (indywidualna)

Na ćwiczeniach omawialiśmy zagadnienie ewolucji czasowej „automatu komórkowego”. Modelem tego zagadnienia jest siatka, w której wartość funkcji węźle jest średnią ważoną otaczających go węzłów i tak:

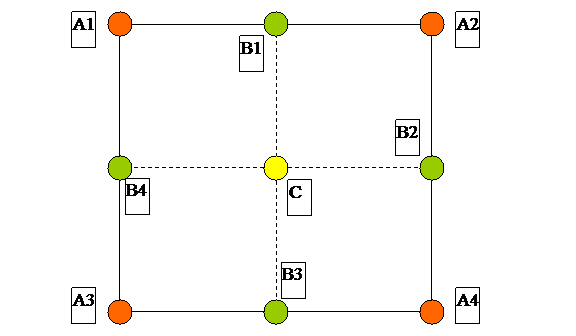
WpływA = 0.8 * (A1(stare)+A2(stare)+A3(stare)+A4(stare))

WpływB = 1.2 * (B1(stare)+B2(stare)+B3(stare)+B4(stare))

C(nowe) =  ( C(stare) + WplywA + WplywB ) / 9

W każdym kroku „ewolucji czasowej” powyższe obliczenia wykonywane są dla każdego wewnętrznego punktu siatki. Zakłada się, ze punkty brzegowe pozostają niezmienione.

Zakłada się że w chwili t₀ zmienione zostają wartości brzegowe wyzerowanej siatki i tak zmienione wartości brzegowe pozostają stałe. Ostatecznym wynikiem ewolucji czasowej jest stabilna siatka, w której dla każdego punktu wewnętrznego nie zachodzą już zmiany wartości, tzn. |C(stare) – C(nowe)| < ε.

Zadanie domowe polega na:

a) zaimplementowaniu powyższego modelu tak aby mógł on być wykonywany na 1-12 procesorów tulipana

b) przeprowadzeniu eksperymentów mających na celu ocenę efektywności implementacji

c) zakładamy,  że w momencie t₀ wartości niezerowe pojawiają się przynajmniej na dwu brzegach siatki, oraz, że przynajmniej jeden narożnik siatki pozostaje zerowy; natomiast ε = 0.001.

Istotne: zmiany na brzegu jak i wielkosc siatki nalezy tak dobrac aby wyniki czasowe mialy sens!!!!!

Wynikiem ma być raport, który dokładnie opisze przeprowadzone eksperymenty praz ich wyniki, oraz będzie posiadał jako załącznik kod programu.

Termin wykonania pracy domowej i metoda dostarczenia: godzina 17:00 (czasu Polskiego), w poniedziałek 19 stycznia, 2004; tekst w formacie: pdf, doc, rtf lub ps, przesłany e-mailem do mnie: marcin@amu.edu.pl.

Powrót do strony "syllabus"