Document encoding: Central European (Win 1250)
![]() wybranie i uzgodnienie zjawiska, które jest badane (wskazanie
istotnych cech)
wybranie i uzgodnienie zjawiska, które jest badane (wskazanie
istotnych cech)
![]() ustalenie okresu czasu, przez który dane będą zbierane
ustalenie okresu czasu, przez który dane będą zbierane
![]() zaprojektowanie czytelnej formy arkusza - łatwej w interpretacji
i wygodnej w użyciu
zaprojektowanie czytelnej formy arkusza - łatwej w interpretacji
i wygodnej w użyciu
![]() zbieranie danych i wypełnianie arkusza (stosowanie jednolitej
techniki zliczania)
zbieranie danych i wypełnianie arkusza (stosowanie jednolitej
techniki zliczania)
![]() wypełnienie dodatkowych kolumn arkusza, które zawierają
podsumowania i wyniki zagregowane, opracowane na podstawie rubryk
podstawowych
wypełnienie dodatkowych kolumn arkusza, które zawierają
podsumowania i wyniki zagregowane, opracowane na podstawie rubryk
podstawowych
| Obserwator: K.Rzepka | Nr komputera: 148 | Data: 21-03-1996 | ||
| Liczba obserwacji: 95 | Zliczenia | Razem | Procent | |
| Komputer pracuje | 55 | 57,9 | ||
| Komputer nie pracuje | naprawa | 5 | 5,3 | |
| brak zadań | 12 | 12,6 | ||
| nie ma operatora | 10 | 10,5 | ||
| awaria systemu | 13 | 13,7 | ||
| Procent |
pola z podsumowaniem -
![]() określenie liczności próbki -
określenie liczności próbki - ![]()
![]() wyznaczenie zakresu zmienności danych czyli rozstępu w próbce
-
wyznaczenie zakresu zmienności danych czyli rozstępu w próbce
- ![]()
![]() podzielenie zakresu zmienności na pewną liczbę przedziałów w
zależności od liczby pomiarów pierwotnych (zwykle na 6 do 12
przedziałów)
podzielenie zakresu zmienności na pewną liczbę przedziałów w
zależności od liczby pomiarów pierwotnych (zwykle na 6 do 12
przedziałów)
![]() określenie szerokości przedziału - najlepiej jednakowej dla
wszystkich
określenie szerokości przedziału - najlepiej jednakowej dla
wszystkich
![]() wyznaczenie granic dla przedziałów (zapewnienie jednoznaczności
przypisania pomiaru do przedziału)
wyznaczenie granic dla przedziałów (zapewnienie jednoznaczności
przypisania pomiaru do przedziału)
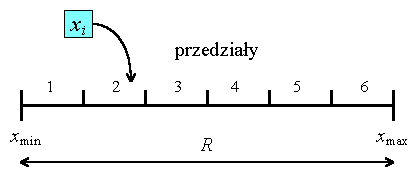
![]() wyznaczenie liczb pomiarów w poszczególnych przedziałach -
opracowanie tablicy rozkładu
wyznaczenie liczb pomiarów w poszczególnych przedziałach -
opracowanie tablicy rozkładu
| Numer przedziału | Zakres przedziału (granice) | Liczba pomiarów -częstość | Częstość skumulowana | Częstość względna | Względna częstość skumulowana |
| 1 | 9,1<=x<9,3 | 1 | 1 | 0,02 | 0,02 |
| 2 | 9,3<=x<9,5 | 5 | 6 | 0,10 | 0,12 |
| 3 | 9,5<=x<9,7 | 4 | 10 | 0,08 | 0,20 |
| 4 | 9,7<=x<9,9 | 11 | 21 | 0,22 | 0,42 |
| 5 | 9,9<=x<10,1 | 13 | 34 | 0,26 | 0,68 |
| 6 | 10,1<=x<10,3 | 10 | 44 | 0,20 | 0,88 |
| 7 | 10,3<=x<10,5 | 4 | 48 | 0,08 | 0,96 |
| 8 | 10,5<=x<10,7 | 0 | 48 | 0,00 | 0,96 |
| 9 | 10,7<=x<=10,9 | 2 | 50 | 0,04 | 1,00 |
| 50 | Razem | 1,00 |
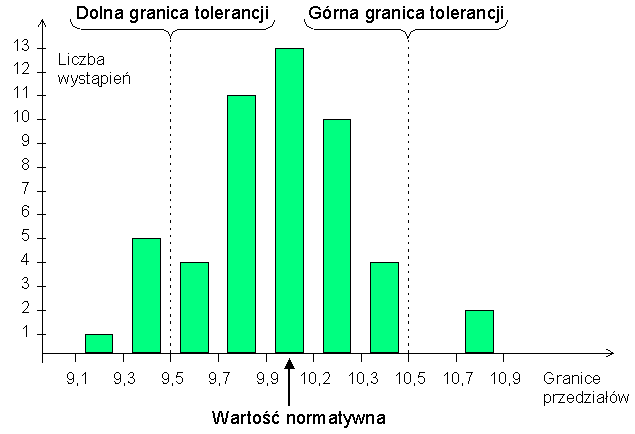
![]() DGT oznacza dolną granicę tolerancji
DGT oznacza dolną granicę tolerancji
![]() GGT oznacza górną granicę tolerancji
GGT oznacza górną granicę tolerancji
![]() przyjęto, że wartość normatywna położona jest pośrodku
przedziału tolerancji
przyjęto, że wartość normatywna położona jest pośrodku
przedziału tolerancji
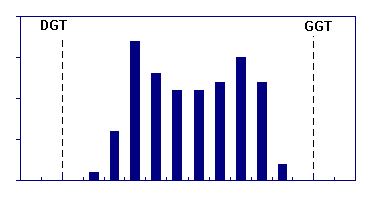 |
nałożone dwa histogramy "normalne" |
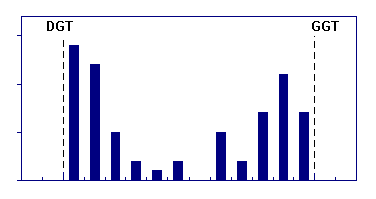 |
nałożone i obcięte dwa histogramy "normalne" |
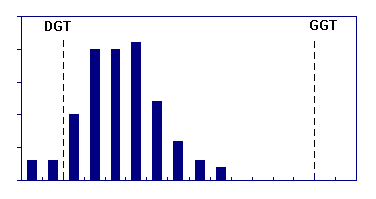 |
przesunięty histogram "normalny" |
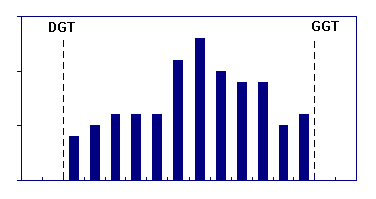 |
mało skupiony i obcięty histogram "normalny" |
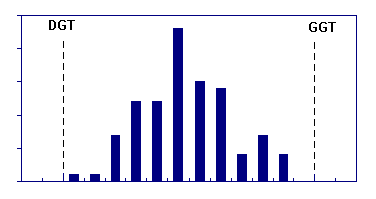 |
histogram "normalny" |
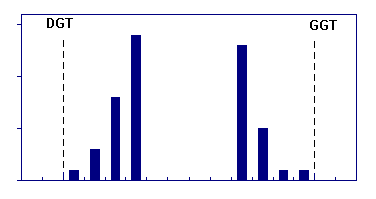 |
wycięty histogram "normalny" |
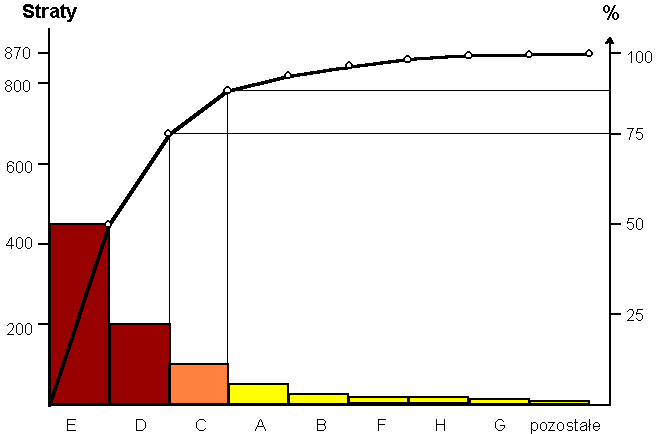
![]() analizę możliwości uzyskania poprawy jakości przy
ograniczonych nakładach
analizę możliwości uzyskania poprawy jakości przy
ograniczonych nakładach
![]() wskazanie grupy najważniejszych przyczyn
wskazanie grupy najważniejszych przyczyn
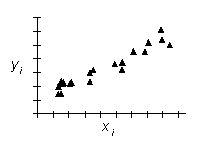
![]() wykrycie związku przyczynowo-skutkowego pomiędzy dwoma
mierzalnymi cechami (korelacja pozytywna, negatywna lub jej brak)
wykrycie związku przyczynowo-skutkowego pomiędzy dwoma
mierzalnymi cechami (korelacja pozytywna, negatywna lub jej brak)
![]() wykrycie par danych
wykrycie par danych ![]() , które odbiegają od korelacji wykazywanej przez większość
pozostałych par
, które odbiegają od korelacji wykazywanej przez większość
pozostałych par
 |
 |
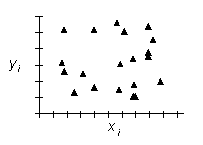 |
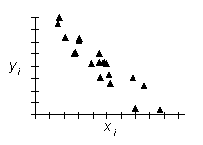
| korelacja pozytywna | korelacja negatywna | brak korelacji |
![]() średnia
arytmetyczna
średnia
arytmetyczna 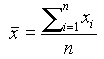 - miara wartości przeciętnej
- miara wartości przeciętnej
![]() rozstęp (zakres)
rozstęp (zakres) ![]() - miara bezwzględnego rozrzutu
- miara bezwzględnego rozrzutu
![]() odchylenie standardowe
odchylenie standardowe 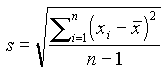 - miara względnego rozrzutu
- miara względnego rozrzutu
![]() współczynnik zmienności
współczynnik zmienności 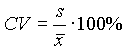 - względna miara rozrzutu
- względna miara rozrzutu
![]() współczynnik skośności
współczynnik skośności 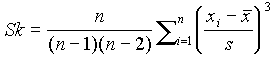 - miara symetrii rozkładu
- miara symetrii rozkładu
![]() mediana
mediana ![]() dla n nieparzystego i
dla n nieparzystego i 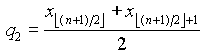 dla n parzystego - miara wartości
przeciętnej
dla n parzystego - miara wartości
przeciętnej
(symbol ![]() oznacza największą z liczb całkowitych
mniejszych lub równych a)
oznacza największą z liczb całkowitych
mniejszych lub równych a)
![]() zakres międzykwartylowy
zakres międzykwartylowy ![]() - miara rozrzutu
- miara rozrzutu
![]() dolny kwartyl
dolny kwartyl ![]() dla n+1 podzielnego przez 4 i
dla n+1 podzielnego przez 4 i 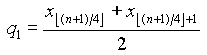 w pozostałych
przypadkach
w pozostałych
przypadkach
![]() górny
kwartyl
górny
kwartyl ![]() dla n+1 podzielnego przez 4 i
dla n+1 podzielnego przez 4 i 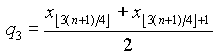 w pozostałych
przypadkach
w pozostałych
przypadkach
![]() współczynnik skośności Pearsona
współczynnik skośności Pearsona 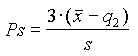 - miara symetrii rozkładu
- miara symetrii rozkładu
![]() moda (dominanta) d = wartość najczęściej występująca
w próbce - miara wartości przeciętnej
moda (dominanta) d = wartość najczęściej występująca
w próbce - miara wartości przeciętnej
| Numer przedziału | Granice przedziału | Wartość centralna | Częstość | Częstość skumulowana |
| 1 | ||||
| ... | ... | ... | ... | ... |
| i | ||||
| ... | ... | ... | ... | ... |
| m |
![]() oszacowanie średniej
oszacowanie średniej 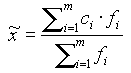
![]() oszacowanie odchylenia standardowego
oszacowanie odchylenia standardowego 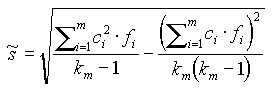
![]() oszacowanie mediany
oszacowanie mediany 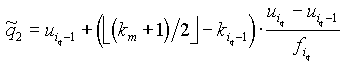 , gdzie dla przedziału iq
zachodzi
, gdzie dla przedziału iq
zachodzi ![]()
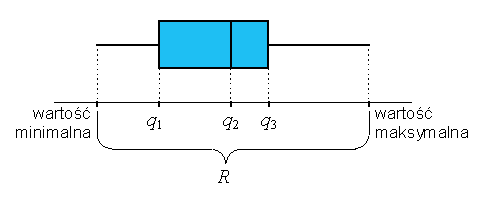
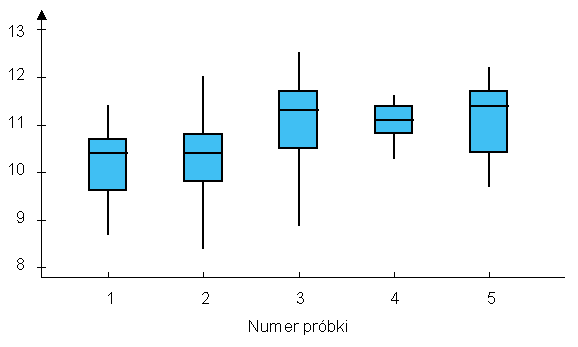
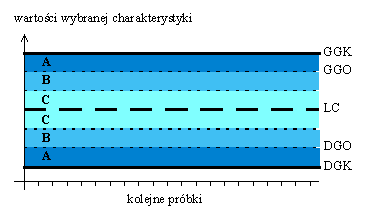
![]() linia centralna - LC
linia centralna - LC
![]() dolna granica kontrolna - DGK
dolna granica kontrolna - DGK
![]() górna
granica kontrolna - GGK
górna
granica kontrolna - GGK
![]() dolna granica ostrzegawcza - DGO
dolna granica ostrzegawcza - DGO
![]() górna
granica ostrzegawcza - GGO
górna
granica ostrzegawcza - GGO
![]() strefy kontrolne - A, B i C
strefy kontrolne - A, B i C
![]() rozróżniania kiedy mamy do czynienia z naturalnym, a kiedy z
nadzwyczajnym rozkładem wyników w próbce
rozróżniania kiedy mamy do czynienia z naturalnym, a kiedy z
nadzwyczajnym rozkładem wyników w próbce
![]() wykrywania kiedy na kontrolowany proces miały wpływ normalne, a
kiedy szczególne przyczyny zmienności
wykrywania kiedy na kontrolowany proces miały wpływ normalne, a
kiedy szczególne przyczyny zmienności
![]() oceny czy proces jest wyregulowany (pod kontrolą statystyczną)
oceny czy proces jest wyregulowany (pod kontrolą statystyczną)
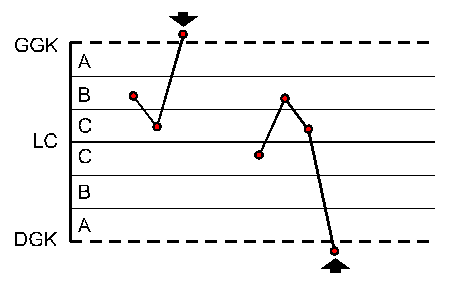 |
pojedynczy punkt poza strefą A |
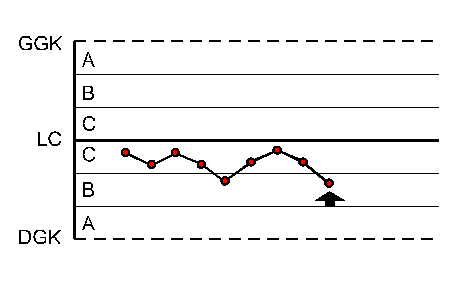 |
9 punktów z rzędu w strefie C lub poza nią po tej samej stronie linii centralnej |
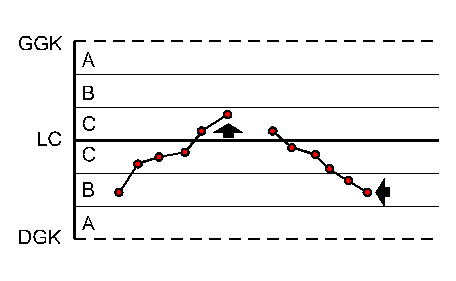 |
6 punktów z rzędu o stale rosnących lub malejących wartościach |
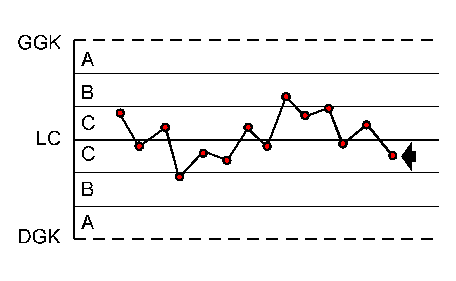 |
14 punktów z rzędu o naprzemiennie rosnących i malejących wartościach |
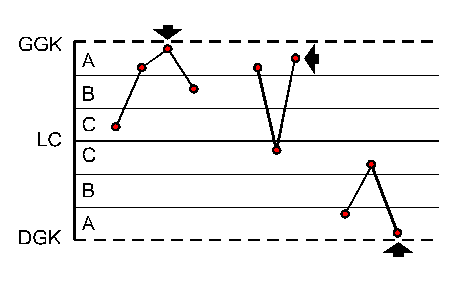 |
2 punkty z 3 kolejnych w strefie A |
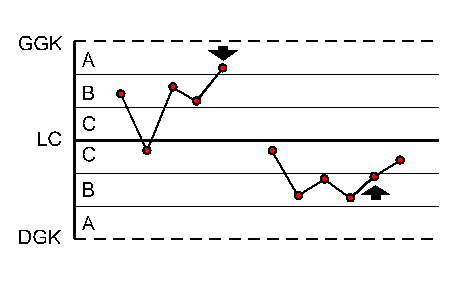 |
4 punkty z 5 kolejnych w strefie B lub A |
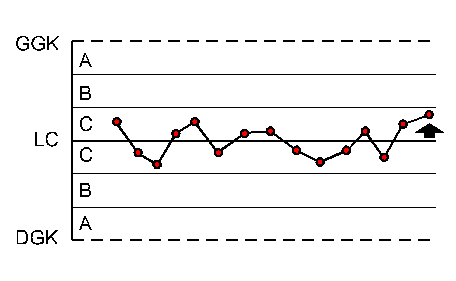 |
15 punktów z rzędu w strefie C (poniżej lub powyżej linii centralnej) |
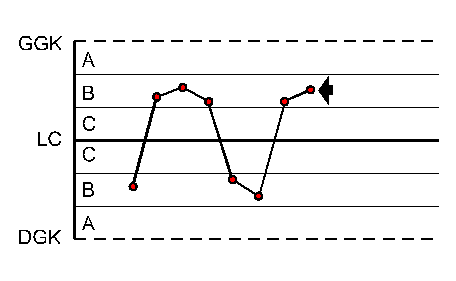 |
8 punktów z rzędu po obu stronach linii centralnej poza strefą C |
| Typ karty | LC | DGK | GGK |
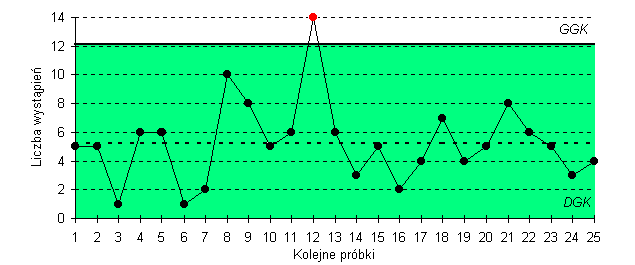
| np | |||
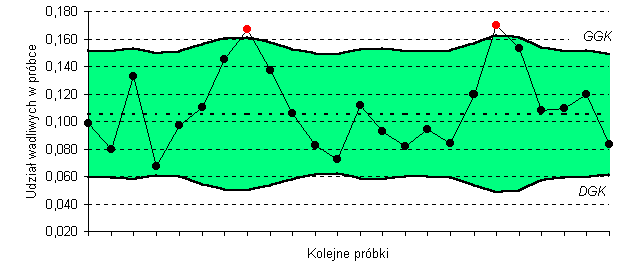
| p | 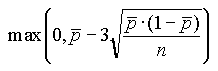 (liczność próbek n jest zmienna) |
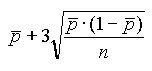 (liczność próbek n jest zmienna) |
|
| c | |||
| u | 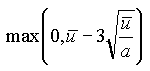 (badany obszar a jest zmienny) |
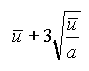 (badany obszar a jest zmienny) |
|
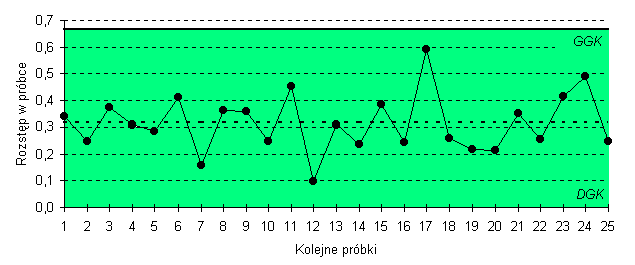
| R | |||
| s |
![]()
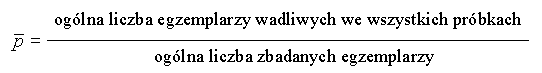
![]()
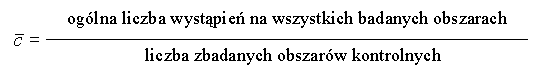
![]()
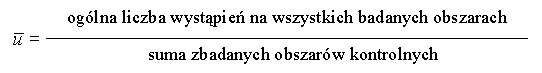
![]()
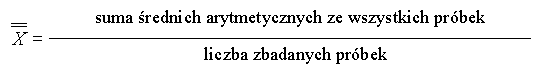
![]()
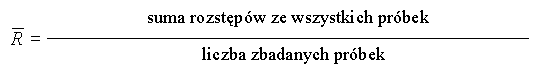
![]()
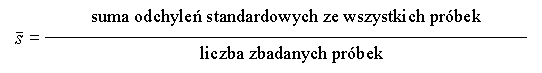
| n | A2 | A3 | D3 | D4 | B3 | B4 |
| 2 | 1,880 | 2,659 | 0 | 3,268 | 0 | 3,267 |
| 3 | 1,023 | 1,954 | 0 | 2,574 | 0 | 2,568 |
| 4 | 0,729 | 1,628 | 0 | 2,282 | 0 | 2,266 |
| 5 | 0,577 | 1,427 | 0 | 2,114 | 0 | 2,089 |
| 6 | 0,483 | 1,287 | 0 | 2,004 | 0,030 | 1,970 |
| 7 | 0,419 | 1,182 | 0,076 | 1,924 | 0,118 | 1,882 |
| 8 | 0,373 | 1,099 | 0,136 | 1,864 | 0,185 | 1,815 |
| 9 | 0,337 | 1,032 | 0,184 | 1,816 | 0,239 | 1,761 |
| 10 | 0,308 | 0,975 | 0,223 | 1,777 | 0,284 | 1,716 |
 |
Tę
stronę czytano |
 |