Project: The algorithms of the computation of the density function

Name: Zizhong Wang (U)

Tingwei Lu (G)

Yanmei Zhang (G)

Considering the following chaotic dynamic system:

(1.1)

S: [0,1] ® [0,1]. Suppose we want to compute the frequency on a set :

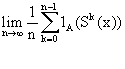(1.2)

where (1.3)

According to Boltzmann's ergodic theory, the time average equals to the space average, as:

(1.4)

where is an invariant measure. If the density function f(x) of m is in , that is f (x) is a fixed point of the Frobenious-Perron operator , that is:

(1.5)

If we get f(x), then we can easily compute:

(1.6)

So, the main problem is compute f(x). We may study various techniques to solve the equation (5) .

2. The Frobenius-Perron operator

For the "logistic model" of population dynamic system:

S(x)=4x(1-x) (2.1)

x Î [0,1]. With (1.1), we take an initial point . We will find the outputs may be any points in [0,1] and the distribution is "chaotic". This is the famous example of chaotic dynamic system. The basic characteristic of the chaotic system is the eventually "uncertainty" and sensitive to the initial point.

If we study the system of (2.1) and (1.1) by statistical view (1.2), we find it behaves "certainty." In other words, the frequency in (1.2) is not sensitive to the and it should equal to (1.4).

We introduce the Frobenious-Perron operator as follow:

Definition 2.1:

let (C ,L ,m ) be a measure space and S: C ® C be a non-singular transformation. The operator : ® defined by

(2.2)

is called the Frobenius-Perron operator associated with S.

Proposition2.1: (Property of the Frobenius-Perron operator)

(1) P is linear, i. e.,

(2) If f³ 0, then Pf³ 0.

(3)

let (C ,L ,m ) be a measure space and S: C ® C be a non-singular transformation. We say that m is invariant under S ( or equivalently, S is measure-preserving with respect to m ), if hold for all A Î L .

Lemma2.1: Suppose is nonnegative, if and only if

(2.3)

is invariant on S.